Martin's Mappings (Hopalong) Barry Martin from Aston University (Birmingham/England) discovered a new variety of strange attractors in the mid-80's. He called them Martin's mappings. A. K. Dewdney presented Martin's first images and the algorithm in his Computer Recreations column in Scientific American (Sept.1986). Dewdney called Martin's new attractor Hopalong, referring to the unique way it grows on the computer screen: the pixels hop from one point to another. Hopalongs don't slowly grow line by line as the popular Mandelbrot fractals do but rather emerge from the whole of the screen at once, getting more and more detailed. They usually grow endlessly into all directions, showing surprising details and structures, often reminiscent of organic structures or oriental rugs. HOP features the original Hopalong attractor and introduces about two dozen new variations on the formula, all similar in structure, but different in detail. The result is a wide variety of new fractals.

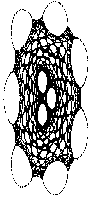Gumowski/Mira CERN physicists Gumowski and Mira found an equally interesting attractor, usually referred to as Mira fractal. Gumowski/Mira type attractors show a somewhat Hopalong-like behaviour although they usually don't grow forever. Some of them are mysteriously similar to diatoms, radiolarians, or other unicellular microorganisms. HOP features the original Gumowski/Mira attractor and introduces a dozen of unique new variations.

The character of the attractor images is quite different from what most people associate with fractals, and in fact, Hopalongs and Miras aren't fractals in the strict mathematical sense. They are plots of orbits of two-dimensional dynamic systems and could maybe referred to as orbit fractals.

Hopalong and Mira fractals show no self-similarity, and they lack the infinite complexity of the famous Mandelbrot Set. On the other hand, the way they are created is far more interesting to watch in real-time than the (usually boring) line-by-line growth of static Mandelbrot images.

HOP's special effect sections feature other loosely fractal- or complexity-related formulas such as Plasma clouds, Connett Circles and Ant Automaton cellular automata.